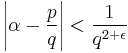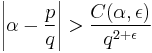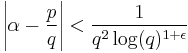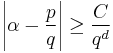Thue–Siegel–Roth theorem
In mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very good'. Over half a century, the meaning of very good here was refined by a number of mathematicians, starting with Liouville in 1844 and continuing with work of Axel Thue (1909), Carl Ludwig Siegel (1921), Dyson (1947), and Klaus Roth (1955).
Contents |
Statement
The Thue–Siegel–Roth theorem states that any irrational algebraic number α has approximation exponent equal to 2, i.e., for given ε > 0, the inequality
can have only finitely many solutions in integers p and q, as was conjectured by Siegel. Therefore any irrational algebraic α satisfies
with C(α,ε) a positive number depending only on ε > 0 and α.
Roth's result is in some sense the best possible, because this statement would fail on setting ε = 0: by Dirichlet's theorem on diophantine approximation there are infinitely many solutions in this case. For comparison, Liouville's theorem has exponent about d, Thue's theorem from 1909 has exponent 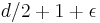 , Siegel's theorem has exponent about 2√d, and Dyson's theorem has exponent about √(2d) where d ≥ 2 is the degree of α. However, there is a stronger conjecture of Serge Lang that
, Siegel's theorem has exponent about 2√d, and Dyson's theorem has exponent about √(2d) where d ≥ 2 is the degree of α. However, there is a stronger conjecture of Serge Lang that
can have only finitely many solutions in integers p and q. If one lets α run over the whole of the set of real numbers, not just the algebraic reals, then both Roth's conclusion and Lang's hold for almost all α. So both the theorem and the conjecture assert that a certain countable set misses a certain set of measure zero.
Proof technique
The proof technique was the construction of an auxiliary function in several variables, leading to a contradiction in the presence of too many good approximations. By its nature, it was ineffective (see effective results in number theory); this is of particular interest since a major application of this type of result is to bounding the number of solutions of some diophantine equations.
Davenport & Roth (1955) showed that Roth's techniques could be used to give an effective bound for the number of rational approximations to algebraic numbers, but not for their sizes. The fact that we do not actually know C(ε) means that the project of solving the equation, or bounding the size of the solutions, is out of reach. Later work using the methods of Alan Baker made some small impact on effective improvements to Liouville's theorem on diophantine approximation, which gives a bound
(see Liouville number); but the inequalities are still weak.
Generalizations
There is a higher-dimensional version, Schmidt's subspace theorem, of the basic result. There are also numerous extensions, for example using the p-adic metric,[1] based on the Roth method. LeVeque generalized the result by showing that a similar bound holds when the approximating numbers are taken from a fixed algebraic number field.[2]:vol. II:iii, 148–152
See also
Notes
- ^ D. Ridout, The p-adic generalization of the Thue-Siegel-Roth theorem, Mathematika, 5, pages 40-48, (1958)
- ^ LeVeque, William J. (2002) [1956]. Topics in Number Theory, Volumes I and II. New York: Dover Publications. ISBN 9780486425399.
References
- Davenport, H.; Roth, Klaus Friedrich (1955), "Rational approximations to algebraic numbers", Mathematika. A Journal of Pure and Applied Mathematics 2: 160–167, doi:10.1112/S0025579300000814, ISSN 0025-5793, MR0077577
- Dyson, Freeman J. (1947), "The approximation to algebraic numbers by rationals", Acta Mathematica 79: 225–240, doi:10.1007/BF02404697, ISSN 0001-5962, MR0023854
- Roth, Klaus Friedrich (1955), "Rational approximations to algebraic numbers", Mathematika. A Journal of Pure and Applied Mathematics 2: 1–20, 168, doi:10.1112/S0025579300000644, ISSN 0025-5793, MR0072182
- Wolfgang M. Schmidt (1980, 1996). "Diophantine approximation". Lecture Notes in Mathematics (Springer) 785. doi:10.1007/978-3-540-38645-2.
- Wolfgang M. Schmidt (1991). "Diophantine approximations and Diophantine equations". Lecture Notes in Mathematics (Springer Verlag) 1467. doi:10.1007/BFb0098246.
- Siegel, Carl Ludwig (1921), "Approximation algebraischer Zahlen", Mathematische Zeitschrift 10 (3): 173–213, doi:10.1007/BF01211608, ISSN 0025-5874
- Thue, A. (1909), "Über Annäherungswerte algebraischer Zahlen", Journal für die reine und angewandte Mathematik 135: 284–305, ISSN 0075-4102, http://resolver.sub.uni-goettingen.de/purl?PPN243919689_0135